In this project we have developed a new algorithm for unsupervised learning of invariances, called slow features analysis (SFA). It is based on the general idea that if a feed-forward network learns to extract slowly varying signals from a continuous input signal, it will learn invariances which are implicitly defined by the input signal: A network trained with moving patterns should learn translation invariance; a network trained with patterns changing in size should learn scale invariance.
The algorithm is based on PCA and differs from the more common online
learning rules in three important aspects:
1. It is guaranteed to find the optimal solution within the considered
class of functions and cannot get stuck in local optima.
2. It yields not only one slowly varying signal, but many uncorrelated
ones, which are ordered by their slowness.
3. It does not scale well with input dimensionality (however, this
disadvantage can be overcome by using hierarchical networks).
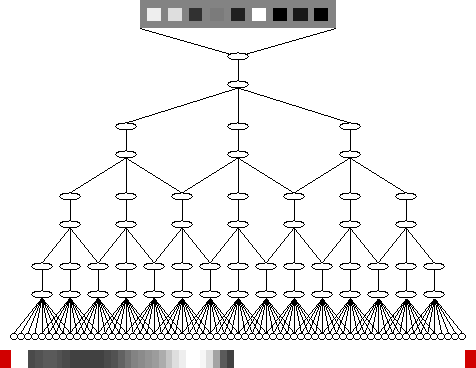
We have used SFA for training a hierachical network as a simple model of the visual system; see Figure 1. The network was based on a one-dimensional retina with 65 sensory units and had eight layers in total. It was trained to learn (the one-dimensional analogue of) translation, scale, rotation, contrast, or illumination invariance, see Animations 1-3, and generalized well to new patterns even when trained with relatively few patterns, such as 10 or 20. Performance degraded if different invariances have to be learned simultaneously.

Figure 1: A hierarchical network as a simple model of the visual system. Each ellipse corresponds to a group of nine units learning to extract slowly varying features from the input signal. Lines between ellipses indicate full connectivity. The bottom layer is the input layer and models a one-dimensional retina. A typical input consists of a random gray-value profile shown below, with the colored blocks indicating the identity of the pattern and the borders of the retina. At the top is shown the activity of the nine output units of the top ellipse ordered by slowness from left to right. The level of activity is indicated by squares of different gray value. In the animations below only the input and output are shown.

Animation 1: Response of a naive network to three patterns shifting across the retina, each pattern indicated by a different color. In this network the 'synaptic weights' have been chosen randomly. The response changes drastically even if the patterns shift by a small amount. Thus this network does not show translation invariance at all. (click on image to get full mpeg animation, 2.1 MB)

Animation 2: Response of a network trained for translation invariance. Several of the output units are fairly invariant to the position of the patterns but sensitive to their identity. Thus the output representation can be used for translation invariant recognition. (click on image to get full mpeg animation, 2.7 MB)

Animation 3: Response of a network trained and tested on patterns varying in size. Here the output units are fairly invariant to the size of the patterns and sensitive to their identity. (click on image to get full mpeg animation, 2.3 MB)
Matlab source code for SFA written by Pietro Berkes is available at http://www.gatsby.ucl.ac.uk/~berkes/software/slowness_model/index.html. Python source code for SFA and several other learning algorithms written by Pietro Berkes and Tiziano Zito is available at http://mdp-toolkit.sourceforge.net/.
Black colored reference are the principal ones. Gray colored references are listed for the sake of completeness only. They contain little additional information. .ps-files are optimized for printing; .pdf-files are optimized for viewing at the computer.